Python小数点桁数🔢 精度を指定して計算！

Pythonでは、小数点以下の桁数や精度を指定して計算することが重要な場面が多く存在します。特に金融や科学計算の分野では、正確な数値処理が求められるため、適切な方法で小数点を扱う必要があります。この記事では、Pythonで小数点以下の桁数を制御し、精度を維持しながら計算を行う方法について詳しく解説します。組み込みモジュールやフォーマット指定子を使ったテクニックを通じて、効率的かつ正確な数値処理を実現する方法を学びましょう。

Pythonにおける小数点以下の桁数と精度の制御方法

Pythonで小数点以下の桁数を指定して計算を行う際、精度の管理は非常に重要です。特に浮動小数点数を取り扱う場合、丸め誤差や表示形式が予期しない結果を引き起こす可能性があります。ここでは、その具体的な操作方法について詳しく解説します。

Pythonでの小数点以下の基本的な設定方法

1. round関数: Pythonにはround()という組み込み関数があり、小数点以下の桁数を簡単に丸めることができます。例えば、round(3.14159, 2)は「3.14」となります。
2. フォーマット指定子: {:.2f}.format(3.14159)のように書式指定を使用すると、表示上の桁数を明示的に制御可能です。
3. f文字列: Python 3.6以降では、f{3.14159:.2f}のようなf文字列が利用でき、簡潔に桁数を調整できます。

Decimalモジュールによる高精度計算

1. Decimalの利点: 標準ライブラリのdecimalモジュールを利用することで、浮動小数点演算における誤差を最小限に抑えることが可能です。
2. 精度の設定: decimal.getcontext().prec = 5とすることで、全体の有効桁数を5桁に制限できます。
3. 実用例: Decimal('3.14159') + Decimal('2.71828')は、正確な結果「5.85987」を返します。

NumPyを使った数値計算と精度管理

1. dtypeの指定: NumPy配列を作成する際に、dtype=np.float64やdtype=np.float32でデータ型を指定できます。
2. around関数: numpy.around(array, decimals=2)を使用して、配列内の要素を小数点以下2桁に丸められます。
3. 適用範囲: 科学技術計算や大規模データ処理において、NumPyは高速かつ高精度な演算を提供します。

数学的関数と小数点以下の精度への影響

1. 三角関数: math.sin()やmath.cos()など、数学モジュールの関数は浮動小数点誤差を持つことがあります。
2. 対策: 誤差を考慮し、適切な丸めやDecimalの使用を検討することが推奨されます。
3. 事例: 例として、math.sqrt(2)の結果は「1.4142135623730951」となりますが、必要な桁数のみ取り出すことで実用性が向上します。

エラーハンドリングと精度に関する注意点

1. OverflowとUnderflow: 非常に大きい値や小さい値を扱う場合、オーバーフローやアンダーフローが発生するリスクがあります。
2. 例外処理: try-exceptブロックを使用して、演算時のエラーを適切にキャッチすることが重要です。
3. デバッグのヒント: sys.float infoを利用して、システムの浮動小数点数の限界値を確認できます。

Pythonの浮動小数点の精度は？

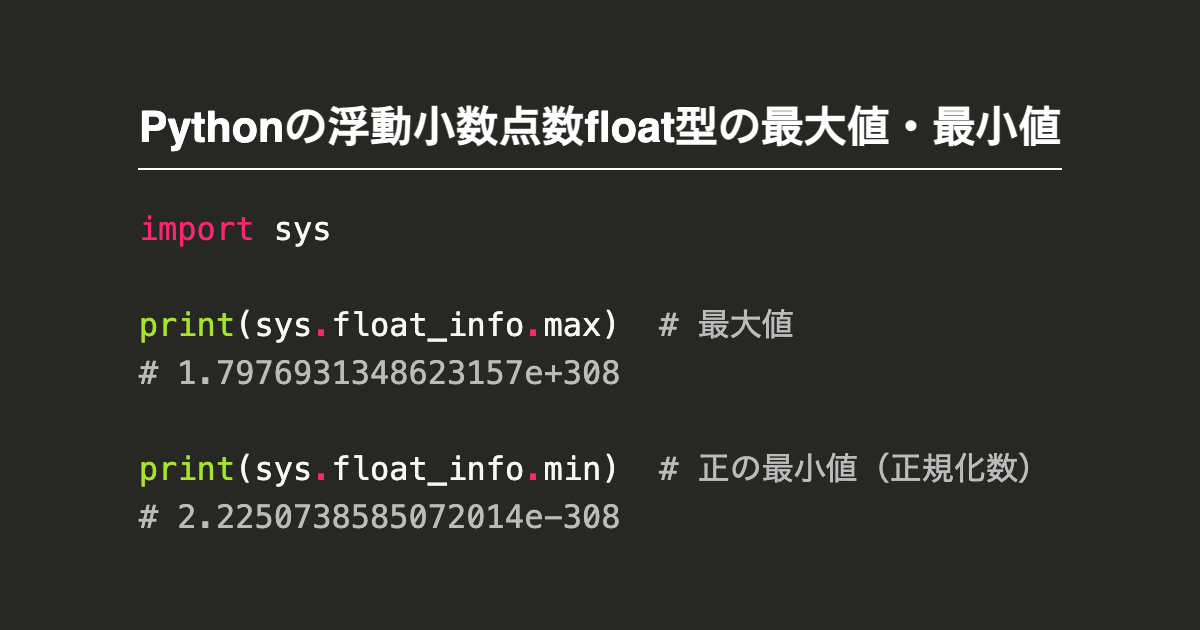
Pythonの浮動小数点の精度は、主にIEEE 754規格に基づく倍精度（64ビット）形式で表現されます。これにより、約15〜16桁の10進数の精度が保証されています。ただし、浮動小数点演算では丸め誤差が発生する可能性があるため、厳密な計算が必要な場合には注意が必要です。

浮動小数点数の内部表現

Pythonの浮動小数点数は、コンピュータ内部でどのように保存されているのでしょうか？
IEEE 754規格に基づき、64ビット中、1ビットは符号、11ビットは指数部、52ビットは仮数部として使用されます。この構造により、非常に広い範囲の数値を効率的に表現できます。

1. 符号ビット: 正負を決定します（0は正、1は負）。
2. 指数部: 数値のスケールを表し、-1022から1023の範囲を持ちます。
3. 仮数部: 有効数字を保持し、52ビットで精度を提供します。

浮動小数点の限界とエラー

浮動小数点を使用する際にはどのような問題が発生するのでしょうか？
丸め誤差や桁落ちが典型的な課題です。特に極端に小さな数値や大きな数値を扱う場合、正確性が損なわれる可能性があります。

1. 丸め誤差: 計算結果が有限のビット幅に収まらない場合に発生します。
2. 桁落ち: 近接した値同士の引き算で有効数字が減少する現象です。
3. オーバーフロー/アンダーフロー: 表現可能な範囲を超えた場合、値が無限大またはゼロとして処理されます。

高精度計算の代替手段

Pythonでより高い精度が必要な場合はどのような方法が利用可能でしょうか？
標準ライブラリ以外にも、DecimalモジュールやFractionモジュールといったツールが用意されています。これらのモジュールは低速ですが、精度重視の場面で役立ちます。

1. Decimalモジュール: 固定小数点および浮動小数点の高精度演算をサポートします。
2. Fractionモジュール: 分数形式での正確な計算を可能にします。
3. サードパーティ製ライブラリ: 例として、mpmathのような任意精度演算ライブラリも活用可能です。

Pythonで浮動小数点を整数に変換するには？

Pythonで浮動小数点を整数に変換するには、主に`int()`関数を使用します。この関数は、浮動小数点数の小数部を切り捨てて整数に変換します。例えば、`int(5.7)`は`5`になります。他にも、`math`モジュールのメソッドを使用して、丸めや切り上げ、切り捨てによる変換が可能です。

1. int()関数の基本的な使い方

`int()`関数は最もシンプルな方法であり、小数点以下を無条件に切り捨てる機能を持っています。

1. 構文: `int(浮動小数点数)`。
2. 例: `int(8.9)` → 結果は`8`。
3. 注意点: 小数点以下の値がどれだけ大きくても切り捨てられます。

2. mathモジュールを使った切り上げと切り捨て

`math`モジュールでは、math.floor()（切り捨て）やmath.ceil()（切り上げ）といった関数を利用して、柔軟な変換が可能です。

1. math.floor(): 小数点以下を常に切り捨てます。例: `math.floor(4.9)` → 結果は`4`。
2. math.ceil(): 小数点以下を常に切り上げます。例: `math.ceil(4.1)` → 結果は`5`。
3. インポート方法: `import math`が必要です。

3. 四捨五入での整数への変換

四捨五入を行いたい場合、round()関数を使用することで目的を達成できます。この方法は、近似値として整数化したいケースに適しています。

1. 構文: `round(浮動小数点数)`。
2. 例: `round(2.5)` → 結果は`2`、`round(3.5)` → 結果は`4`。
3. 特徴: `.5`の場合、偶数方向に丸められます（銀行丸め）。

Pythonのfloat32の桁数はいくつですか？

Pythonのfloat32の桁数は約7桁です。これは、IEEE 754規格に基づく単精度浮動小数点形式で表されるためです。

float32の基本仕様とは？

float32は、符号部1ビット、指数部8ビット、仮数部23ビットで構成されます。この形式により、データを効率的に保存し計算が可能です。

1. 符号部は正負を決定します。
2. 指数部では2のべき乗を表現し、値の範囲を広げます。
3. 仮数部は有効数字に関与し、精度を提供します。

なぜfloat32は7桁程度の精度なのですか？

有効数字7桁という特性は、仮数部の23ビットに由来します。具体的には、2進数ベースでの精度を10進数に変換した結果です。

1. 2進数の23ビットは約7桁の10進数に対応します。
2. 誤差が出やすい丸め処理に注意が必要です。
3. 限られたビット数であるため、大きな値や非常に小さな値では精度低下が発生します。

float32を使用する際の注意点

float32はメモリ効率に優れていますが、精度が重要になる場面では注意が必要です。特に金融や科学計算などでの利用には適さない場合があります。

1. 誤差が積み重なると、最終結果が大きくずれる可能性があります。
2. 計算時にオーバーフローやアンダーフローが発生するリスクがあります。
3. 厳密な計算が必要な場合はfloat64などの高精度型を選択することをお勧めします。

Pythonで小数点第一位まで表示するには？

Pythonで小数点第一位まで表示するには、`round()`関数やフォーマット指定子を使用します。たとえば、`round(3.14159, 1)`とすると「3.1」が返されます。また、文字列フォーマットでは、`{:.1f}.format(3.14159)`やf文字列の`f{3.14159:.1f}`を使用することで小数点第一位までの値を表示できます。

Pythonでの四捨五入処理について

`round()`関数は四捨五入を行うための代表的な方法です。小数点以下の桁数を指定して使用します。

1. 基本構文: round(数値, 桁数)。
2. 第二引数に1を指定することで、小数点以下一桁に丸められます。
3. 注意点として、偶数への丸め（バンク型丸め）が行われる場合があるため、予期せぬ結果になる可能性があります。

書式設定による制御方法

文字列フォーマットを使用することで、数値の表示形式を細かく制御できます。

1. f文字列では、`f{変数:.1f}`のように記述します。
2. `format()`メソッドを使う場合は、`{:.1f}.format(変数)`が便利です。
3. どちらも小数点以下1桁に固定され、余分な桁は自動的に丸められます。

データの精度と誤差への対応

浮動小数点数の丸め誤差には特に注意が必要です。

1. 小数点以下の桁を明示的に丸める場合は、計算前後で値をチェックしましょう。
2. Decimalモジュールを使用することで、より正確な演算が可能です。
3. 表示用途であれば、書式設定のみで十分ですが、重要な計算では誤差評価を忘れずに行うことが推奨されます。

よくある質問

Pythonでは小数点以下の桁数をどのように指定しますか？

round関数を使用することで、Pythonでは簡単に小数点以下の桁数を指定できます。例えば、`round(数値, 桁数)`という形式で記述すると、指定した桁数に丸められます。また、Decimalモジュールを利用すれば、より高度な精度の制御が可能です。ただし、浮動小数点数の性質上、丸め誤差が発生する可能性があるため、計算結果には注意が必要です。

なぜPythonで小数点以下の計算が正確ではない場合がありますか？

これは浮動小数点数の内部表現によるものです。コンピュータは2進数で数値を処理するため、10進数で表される小数を完全に表現できない場合があります。その結果、微小な誤差が生じることがあります。これを回避するには、DecimalやFractionといったモジュールを活用し、適切なデータ型を選択することが推奨されます。

Decimalモジュールを使う利点は何ですか？

Decimalモジュールは、高精度な計算が必要な場面で特に役立ちます。通常のfloat型と異なり、Decimalは10進数として数値を扱うため、丸め誤差を最小限に抑えることができます。また、有効桁数や丸め方法を明示的に設定できるため、金融計算や科学技術計算などの分野で非常に信頼性が高いです。ただし、Decimalはパフォーマンスが若干低下する可能性があるため、用途に応じて使い分けることが重要です。

formatメソッドを使って小数点以下の桁数を表示する方法は？

Pythonでは、formatメソッドまたはf文字列を使用して、出力時の小数点以下の桁数を簡単に制御できます。例えば、`{:.2f}.format(数値)`や`f{数値:.2f}`と記述すると、小数点以下2桁まで表示されます。この方法は計算精度には影響を与えませんが、視覚的な桁揃えや見栄えを整える際に非常に便利です。

Toyoda Isoshi